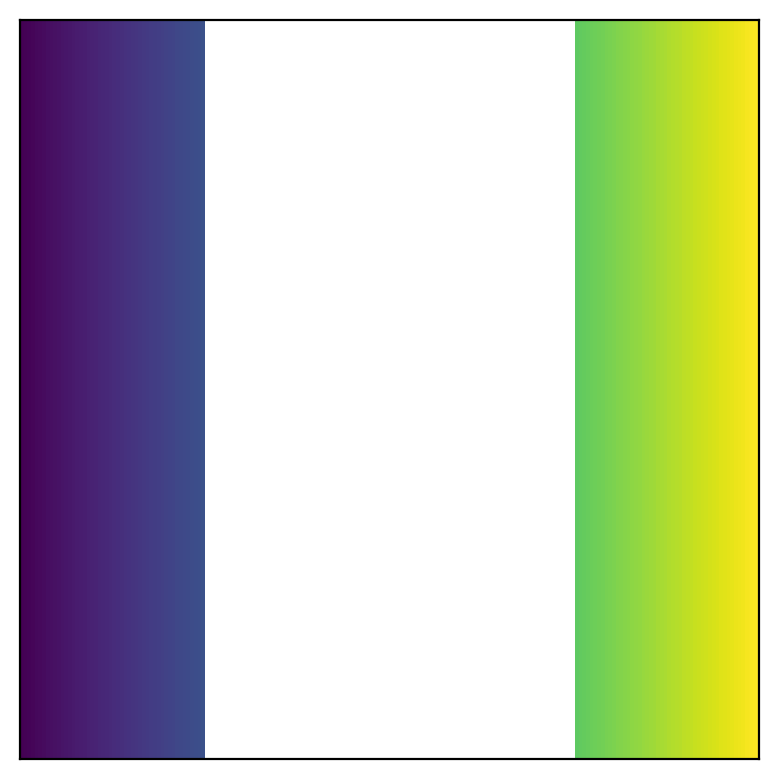DEM void filling algorithms

Here’s a simple 2D numpy array with some NaN pixels.

import numpy as np

size = 200
x = np.linspace(0, 1, size)
y = np.linspace(0, 1, size)
xx, yy = np.meshgrid(x, y)
unfilled[(xx > 0.25) & (xx < 0.75)] = np.nan


To fill the white space with realistic-looking data you need a void filling algorithm. Making things hard to google, this process is sometimes called inpainting, imputation, interpolation or extrapolation.

Different algorithms have different strengths and weaknesses. For interpolating elevation data (DEMs) we’re mostly looking for smooth transitions (as sharp edges are uncommon in natural terrain).

Less-good algorithms

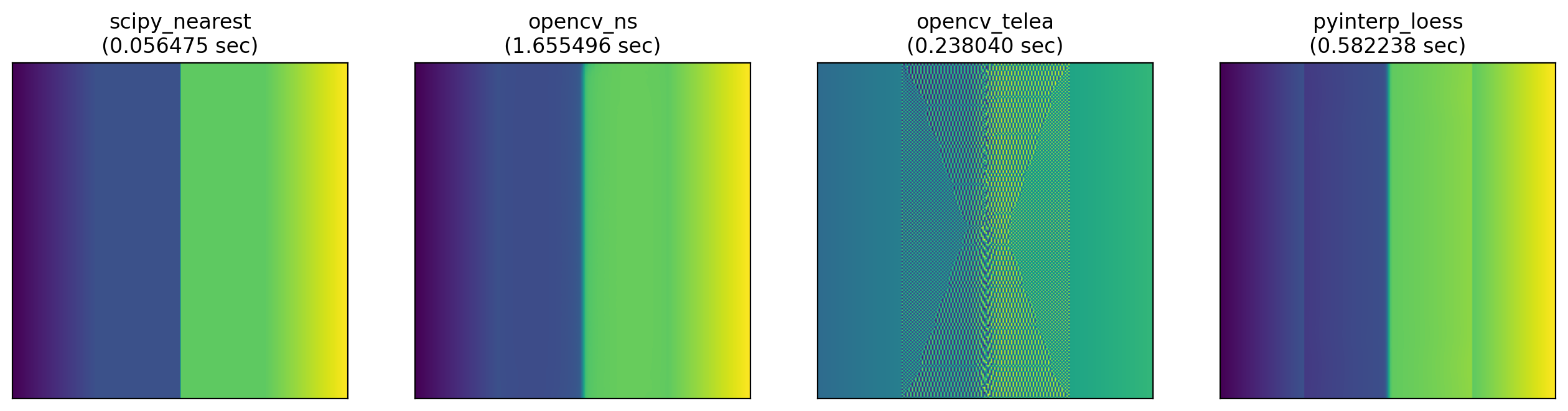
First, the algorithms that couldn’t handle our simple array above.

from scipy.interpolate import NearestNDInterpolator
import pyinterp.fill
import cv2


def scipy_nearest(a):
    mask = np.where(np.isfinite(a))
    interp = NearestNDInterpolator(np.transpose(mask), a[mask])
    return interp(*np.indices(a.shape))


def opencv(a, algo):
    assert algo in {cv2.INPAINT_NS, cv2.INPAINT_TELEA}
    a_min = np.nanmin(a)
    a_max = np.nanmax(a)
    a_norm = (a - a_min) / (a_max - a_min)
    a_norm = a_norm.astype(np.float32)
    
    mask = np.isnan(a).astype(np.uint8)
    a_norm[np.isnan(a_norm)] = 0

    res_norm = cv2.inpaint(a_norm, mask, inpaintRadius=10, flags=algo)
    res = res_norm * (a_max - a_min) + a_min
    return res


def pyinterp_loess(a):
    x_axis = pyinterp.Axis(x, is_circle=False)
    y_axis = pyinterp.Axis(y, is_circle=False)
    grid = pyinterp.Grid2D(x_axis, y_axis, a)
    res = pyinterp.fill.loess(grid, nx=55, ny=55)
    return res

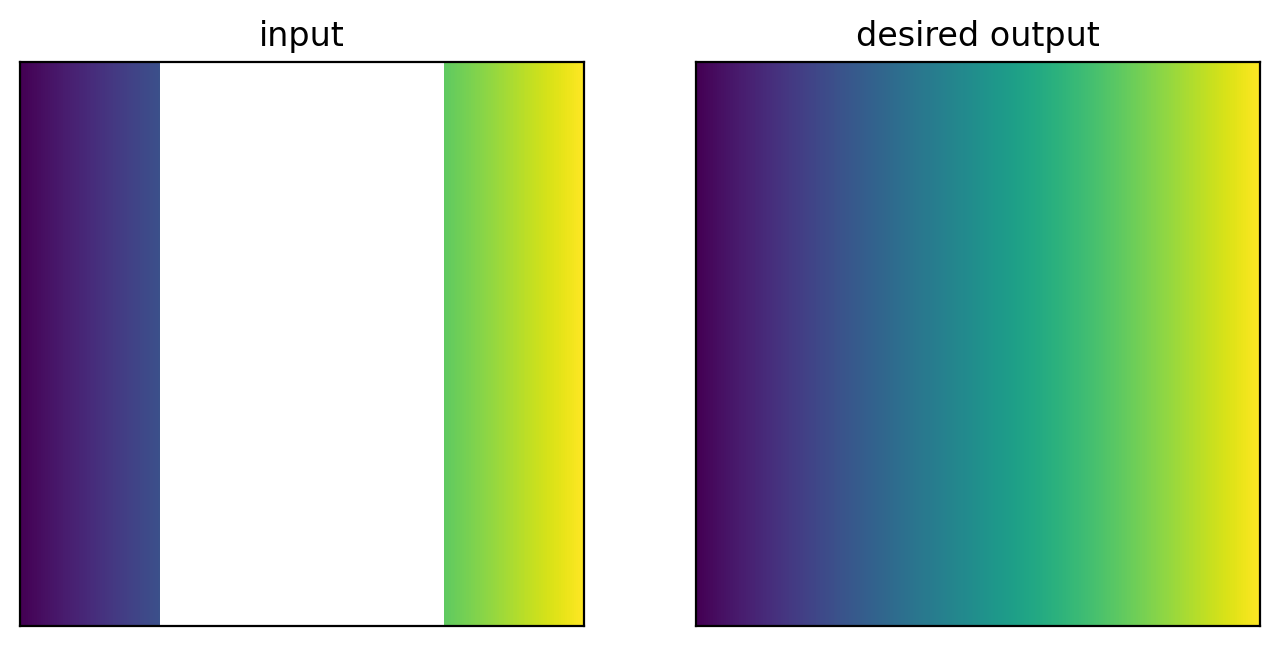
We’re looking for this


but instead get this



In fairness

Better algorithms

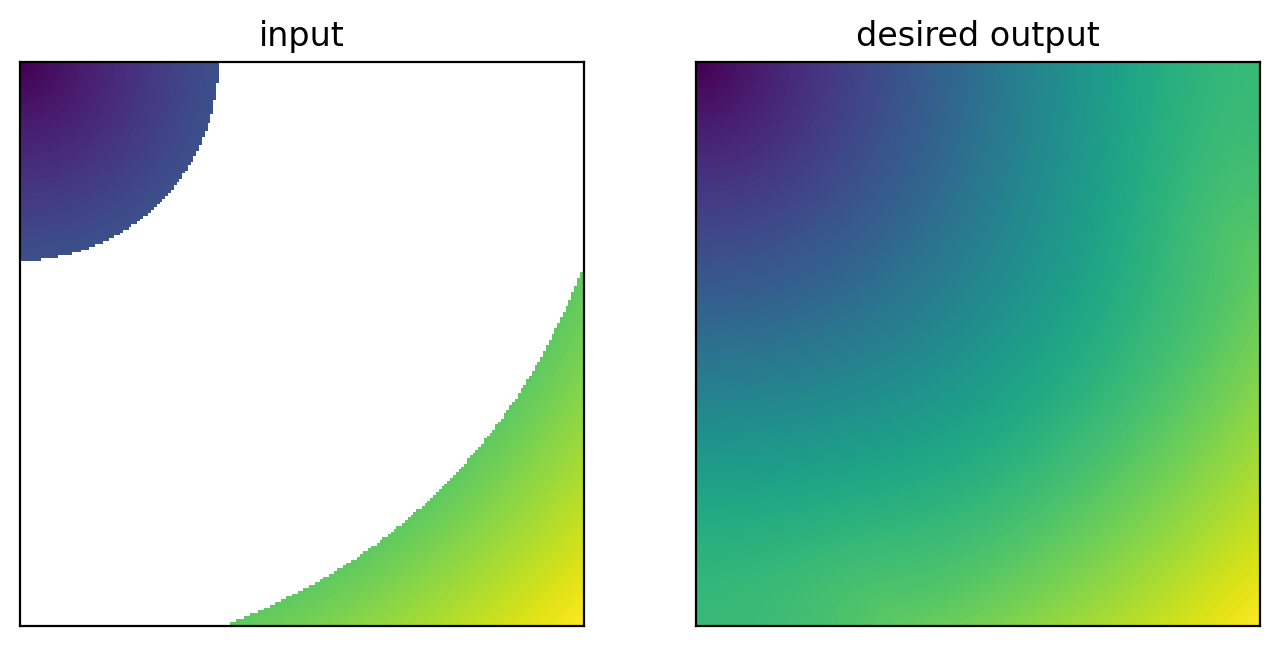
Here’s a more complex shape:

unfilled = np.sqrt(xx**2 + yy**2) / 2**0.5
unfilled[(unfilled > .25) & (unfilled < 0.75)] = np.nan


and the results from the remainder of the algorithms (which all got a perfect score in the simple case above):

from skimage.restoration import inpaint_biharmonic
import rasterio.fill


def fill_rasterio(a):
    mask = np.isfinite(a)
    max_search_distance = int(math.sqrt(a.shape[0] ** 2 + a.shape[1] ** 2)) + 1
    return rasterio.fill.fillnodata(a, mask=mask, max_search_distance=max_search_distance, smoothing_iterations=0)


def fill_skimage_inpaint_biharmonic_region(a):
    mask = np.isnan(a)
    return inpaint_biharmonic(a, mask, split_into_regions=True)


def fill_pyinterp_gauss_seidel(a):
    x_axis = pyinterp.Axis(x,is_circle=False)
    y_axis = pyinterp.Axis(y,is_circle=False)
    grid = pyinterp.Grid2D(x_axis, y_axis, a)
    has_converged, res = pyinterp.fill.gauss_seidel(grid, num_threads=1)
    return res


Rasterio (which uses GDAL’s GDALFillNodata function under the hood) has this weird orthogonal artefacting.

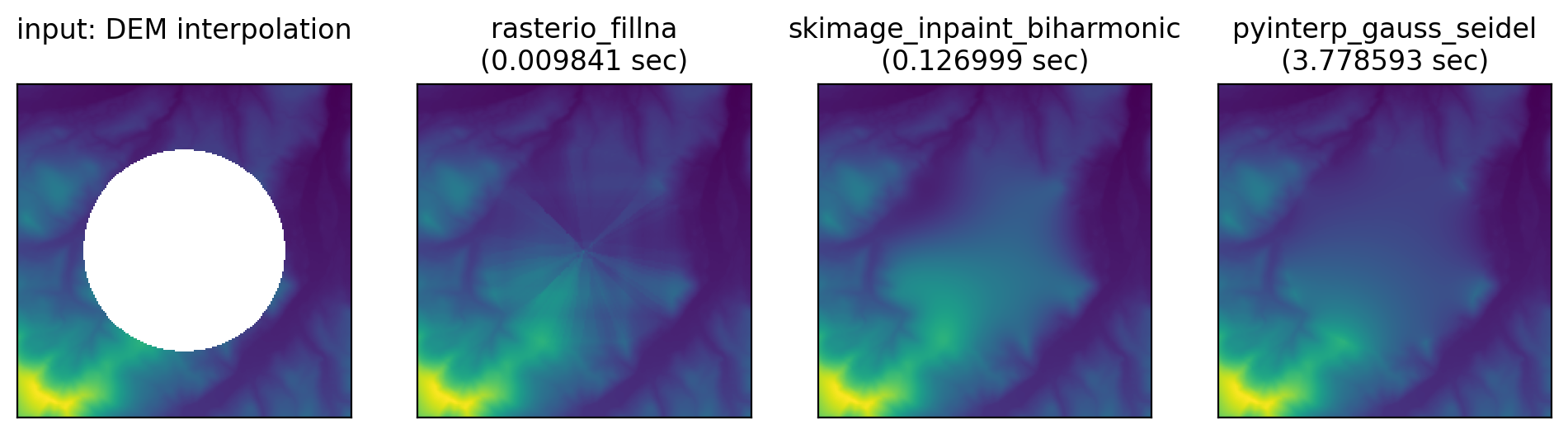
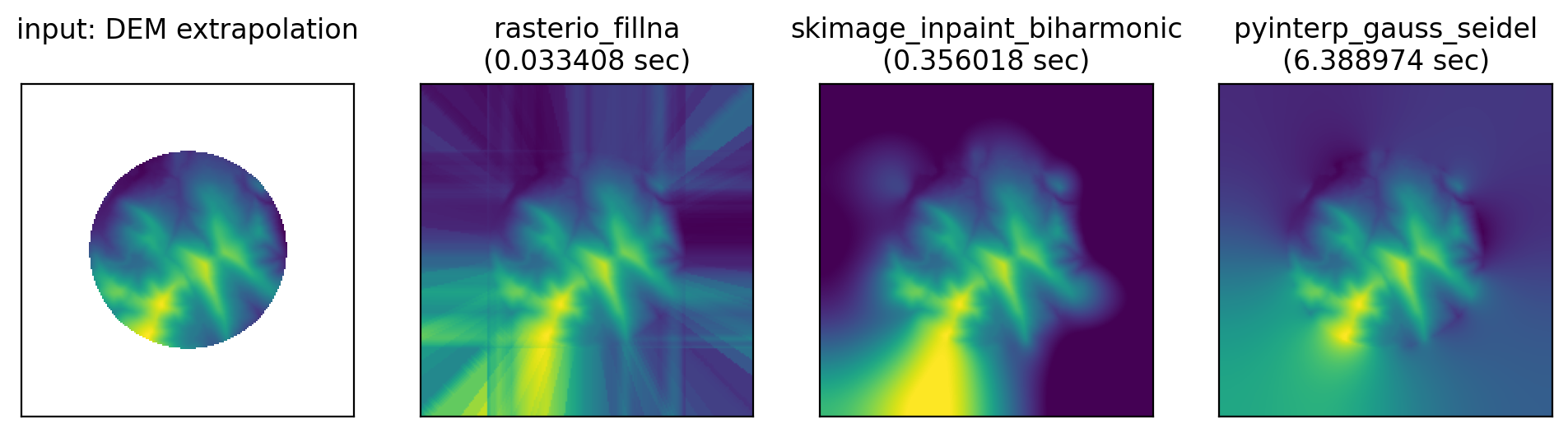
Let’s try an actual DEM:

path = Path("Copernicus_DSM_10_N51_00_W116_00_DEM.tif")
with rasterio.open(path) as f:
    dem = f.read(1)
unfilled = dem[:size, :size]




  • Rasterio / GDAL again adds a bunch of linear artefacts that look nothing like real topography.
  • Skimage’s biharmonic algorithm certainly looks the most like real terrain and is the smoothest. Though both the interpolation and extrapolation result in large areas with a value at the extreme ends of the range of edge pixel values.
  • pyinterp’s Gauss Seidel fill looks more like a patch than realistic terrain, though the filled data tends towards the global mean of the raster/edge, so may better minimise a quantitative error function.

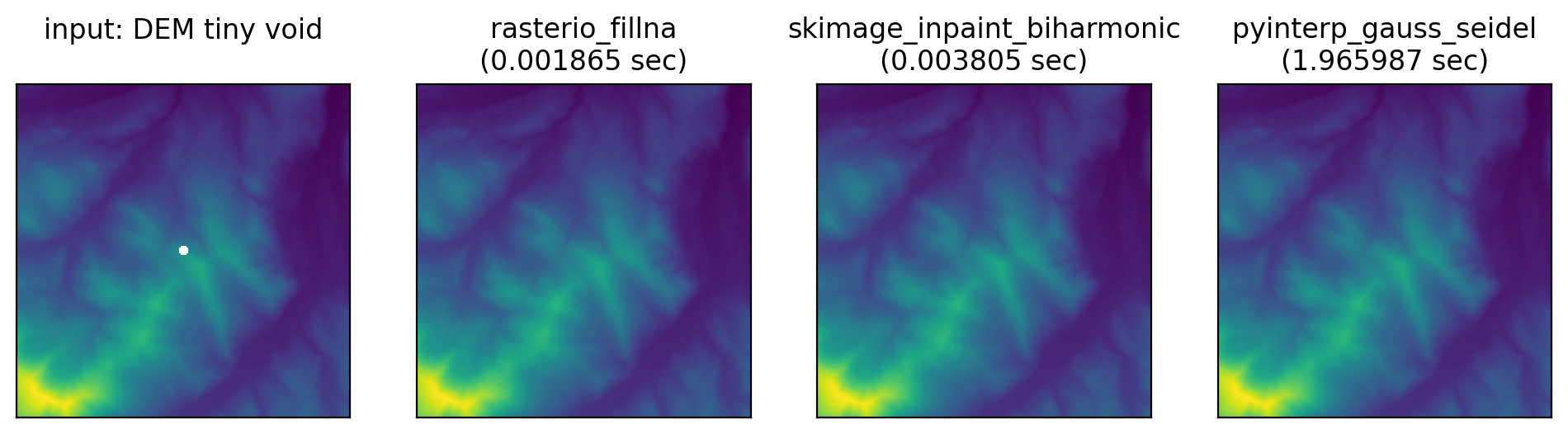
Tiny infill performance

For small void areas the skimage and rasterio are able to do some optimisations to reduce the computation time.



Algorithms not tested

Scipy has lots of different interpolation functionality, but it’s very complex and the recent rewrite of the interpolation API has made it even harder to find examples. I’m fairly sure scipy can’t do gridded interpolation of missing values: it can do void interpolation by treating the pixels as a non-gridded collection of points, but this approach scales badly for large rasters.

Astropy is my usual go-to for arrays with missing data: the library typically handles NaNs by ignoring them rather than propagating them everywhere. You can do filling with astropy but it means convolving a fixed-sized kernel over your array, so it’d be hard to choose an appropriate kernel for voids of different scales.

Finally there are a number of AI tools for infilling, some trained directly on elevation data. But

  • machine learning algorithms are typically rather slow and can’t be sped up for small voids
  • they’re harder to generalise: due to the complexity of AI algorithms you can’t get a robust sense of model performance by inspecting just a few cases like in this blog post
  • complex models are more likely to overfit. For my DEM usecase an underfit model is preferable, as at least a featureless surface communicates lack of certainty while spurious terrain features imply a greater accuracy than than the reality.

Voidless elevation data

GPXZ’s global elevation dataset comes with voids pre-filled: no inpainting necessary!

If you need high-quality elevation data, get in touch at [email protected]!